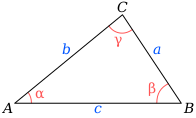
Triangulo
El triángulo es un polígono de tres lados
Un triángulo, en geometría,, es un polígono de tres lados determinado por tres segmentos de tres rectas que se cortan, denominados lados (Euclides); o tres puntos no alineados llamados vértices. También puede determinarse un triángulo por cualesquiera otros tres elementos relativos a él, como por ejemplo un ángulo y dos medianas; o un lado, una altura y una mediana.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
• Los tres ángulos internos de un triángulo miden 180° en geometría euclidiana.[1]
• La suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado.
• El valor de la paralela media de un triángulo (recta que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo.
• Para cualquier triángulo se verifica el Teorema del seno que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»:
Para cualquier triángulo se verifica el Teorema del coseno que demuestra que «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:
Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c, se verifica el