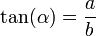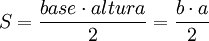Triangulo Rectángulo
Triángulo rectángulo se denomina al triángulo en el que uno de sus ángulos es recto, es decir, mide 90º (grados sexagesimales) o π/2 radianes.
Nombre de sus lados
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
La suma de sus angulos es igual a 180 grados.
Relaciones métricas en un triángulo rectángulo >>>
En un triángulo rectángulo:
La medida de un cateto es media proporcional entre la medida de la hipotenusa y su proyección sobre ella.
-
-
, también se cumple: 
-
La medida de la altura es media proporcional entre los dos segmentos que determina sobre la hipotenusa.
-
-
, es decir: 
-
La relación entre catetos e hipotenusa se establece mediante el Teorema de Pitágoras:
donde
es la medida de la hipotenusa.
Razones trigonométricas en un triángulo rectángulo >>>
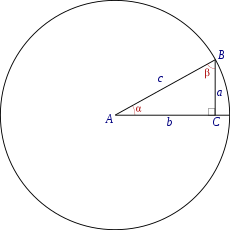
En un triángulo rectángulo, las razones trigonométricas del ángulo
con vértice en A, son:
El seno: la razón entre el cateto opuesto y la hipotenusa,
La tangente: la razón entre el cateto opuesto y el adyacente,
Área de un triángulo rectángulo
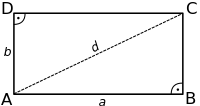
Se puede considerar el área de un triángulo como la mitad del área de un rectángulo partido por su diagonal.
donde y 
son las medidas de los catetos que coinciden con los dos lados y las correspondientes alturas del rectángulo citado.
Además, los catetos coinciden con dos de las tres alturas del propio triángulo.